导数大题一、二问专练
一、求单调性解题步骤:
(1)求函数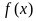 的定义域
的定义域
(2)求函数的导函数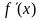 ,并化简;
,并化简;
(3)令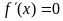 ,求出所有的根,并检查根是否在定义域内。(注意此处是否引出讨论)
,求出所有的根,并检查根是否在定义域内。(注意此处是否引出讨论)
(讨论:1)讨论的对象,即讨论哪个字母参数
2)讨论的引发,即为何讨论
3)讨论的范围,即讨论中要做到“不重不漏”)
(4)列表:注意定义域的划分、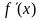 正负号的确定
正负号的确定
(5)根据列表情况作出答案
二、导数难点:
难点一:如何讨论:
(1)判断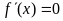 是否有根(可通过判别式的正负来确定),如果无法确定,引发讨论;
是否有根(可通过判别式的正负来确定),如果无法确定,引发讨论;
(2)求完根后,比较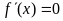 两根的大小,如果无法确定,引发讨论。
两根的大小,如果无法确定,引发讨论。
(3在填表时确定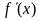 的正负或解不等式
的正负或解不等式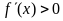 过程中,引发讨论。
过程中,引发讨论。
难点二、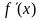 正负的确定
正负的确定
(1) 当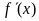 或
或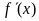 式中未确定部分是一次或二次函数时,画函数图象草图来确定正负号;
式中未确定部分是一次或二次函数时,画函数图象草图来确定正负号;
(2)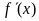 为其他函数时,由
为其他函数时,由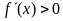 的解集来确定
的解集来确定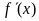 的正负。
的正负。
(3)若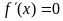 无根或重根,不必列表,直接判断导函数的正负即可。
无根或重根,不必列表,直接判断导函数的正负即可。
题型一:讨论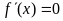 是否有根型
是否有根型
(1)若导数是二次函数,需判断判别式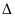 的正负
的正负
(2)若导数是一次函数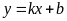 ,需判断
,需判断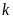 的正负
的正负
1、设函数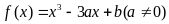 .
.
(Ⅰ)若曲线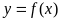 在点
在点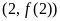 处与直线
处与直线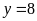 相切,求
相切,求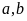 的值;
的值;
(Ⅱ)求函数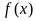 的单调区间与极值点
的单调区间与极值点
2.(08文)已知函数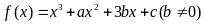 ,且
,且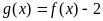 是奇函数.
是奇函数.
(Ⅰ)求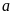 ,
,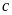 的值;
的值;
(Ⅱ)求函数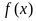 的单调区间
的单调区间
(18)(本小题共13分)已知函数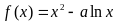 (
(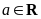 ).(练习)
).(练习)
(Ⅰ)若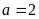 ,求证:
,求证: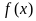 在
在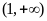 上是增函数;
上是增函数;
(2)求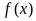 的单调区间;
的单调区间;
18.设函数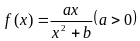 。
。
(1)若函数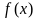 在
在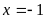 处取得极值
处取得极值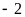 ,求
,求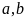 的值;
的值;
(2)求函数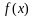 的单调区间
的单调区间
(3)若函数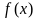 在区间
在区间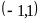 内单调递增,求
内单调递增,求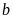 的取值范围
的取值范围
3(2010东城一摸试卷)已知函数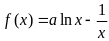 ,
,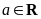
(Ⅰ)若曲线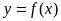 在点
在点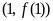 处的切线与直线
处的切线与直线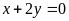 垂直,求
垂直,求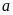 的值;
的值;
(Ⅱ)求函数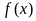 的单调区间;
的单调区间;
4.(本小题满分13分)已知函数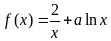 ,
,![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]()
![]() 在区间
在区间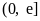 上的最小值.
上的最小值.
5.(安徽)已知函数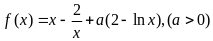 ,求
,求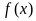 的单调性.
的单调性.
6.已知函数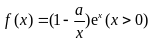 ,其中
,其中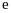 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当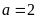 时,求曲线
时,求曲线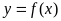 在
在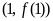 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(II)求函数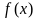 的单调区间
的单调区间
题型二:比较两根大小讨论型
1、设函数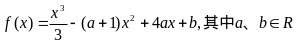 (基础)
(基础)
(Ⅰ)若函数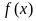 在
在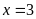 处取得极小值是
处取得极小值是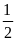 ,求
,求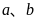 的值;
的值;
(Ⅱ)求函数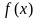 的单调递增区间;
的单调递增区间;
18.(本![]() 小题满分13分)设函数
小题满分13分)设函数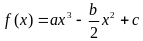 ,其图像过点(0,1).(基础)
,其图像过点(0,1).(基础)
(1)当方程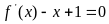 的两个根分别为是
的两个根分别为是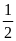 ,1时,求f(x)的解析式;
,1时,求f(x)的解析式;
(2)当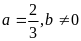 时,求函数f(x)的极大值与极小值.
时,求函数f(x)的极大值与极小值.
2.(天津)已知函数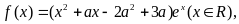 其中
其中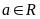 (中等)
(中等)
当
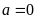 时,求曲线
时,求曲线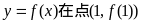 处的切线的斜率;
处的切线的斜率; 求函数
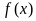 的单调区间与极值。
的单调区间与极值。
18.(2011北京理)已知函数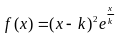 .(偏难)
.(偏难)
(1)求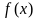 的单调区间;
的单调区间;
(2)若对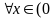 ,
,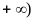 ,都有
,都有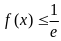 ,求
,求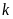 的取值范围。
的取值范围。
18.(本小题共13分)已知函数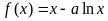 ,
,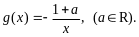
(Ⅰ)若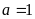 ,求函数
,求函数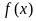 的极值;
的极值;
(Ⅱ)设函数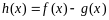 ,求函数
,求函数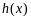 的单调区间;
的单调区间;
综合题(讨论包含一、二两种情况)
18. (本小题共14分)已知函数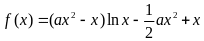 .
.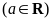 .
.
(I)当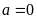 时,求曲线
时,求曲线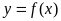 在
在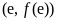 处的切线方程(
处的切线方程(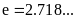 );
);
(II)求函数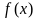 的单调区间
的单调区间
题型三:确定导数正负讨论型
1.设函数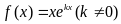
(Ⅰ)求曲线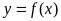 在点
在点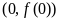 处的切线方程;
处的切线方程;
(Ⅱ)求函数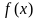 的单调区间;
的单调区间;
2.已知函数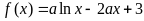 (
(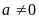 ).
).
(Ⅰ)求函数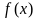 的单调区间;
的单调区间;
题型四:基础无讨论题(必会题)
1(东城·文)(无讨论)
已知函数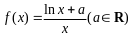 ,
,
⑴若曲线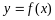 在点
在点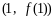 处的切线与直线
处的切线与直线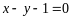 平行,求
平行,求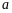 的值;
的值;
⑵求函数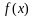 的单调区间和极值;
的单调区间和极值;
2.(本小题共14分)已知函数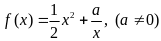 .(无讨论)
.(无讨论)
(Ⅰ)当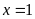 时函数
时函数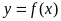 取得极小值,求a的值;
取得极小值,求a的值;
(Ⅱ)求函数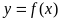 的单调区间.
的单调区间.
18.(本小题满分14分)设函数![]()
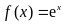 ,其中
,其中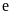 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求函数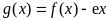 的单调区间;(无讨论)
的单调区间;(无讨论)
18.(本小题满分14分)已知函数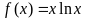 .(文科基础题)
.(文科基础题)
(Ⅰ)求函数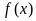 的极值点;
的极值点;
(Ⅱ)若直线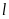 过点
过点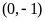 ,并且与曲线
,并且与曲线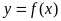 相切,求直线
相切,求直线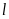 的方程;
的方程;
18.(本小题共14分)已知函数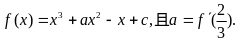 (文科基础题)
(文科基础题)
(I)求a的值;
![]() (II)求
(II)求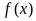 的单调区间;
的单调区间;
17.(本小题满分13分)已知曲线![]() 满足下列条件:
满足下列条件:
①过原点;②在![]() 处导数为-1;③在
处导数为-1;③在![]() 处切线方程为
处切线方程为![]() .
.
(Ⅰ) 求实数![]() 的值;
的值;
(Ⅱ)求函![]() 数
数![]() 的极值
的极值
18. (本小题共14分)已知函数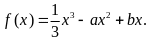
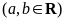 (文科基础题)
(文科基础题)
(I)若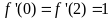 ,求函数
,求函数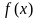 的解析式;
的解析式;
19. 已知函数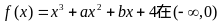 上是增函数,在(0,1)上是减函数.
上是增函数,在(0,1)上是减函数.
(I)求b的值8.